1. 引言
深度强化学习在复杂任务中已经取得了很好的效果。然而,现有的深度Q网络(DQN)存在以下局限性:
1) 记忆能力有限,只能利用最近几帧的信息。
2) 依赖于在每个决策点能够观察到完整的游戏画面。
为了解决这些问题,本文提出了深度递归Q网络(DRQN),通过在DQN中加入长短期记忆(LSTM)来处理部分可观测的环境。
2. 深度Q学习
Q学习是一种用于估计长期回报的无模型离线策略算法。传统Q学习需要维护一个状态-动作值表,而深度Q学习使用神经网络来近似Q值函数:
$$Q(s, a|\theta) \approx Q^*(s,a)$$
其中$\theta$是网络参数。训练时使用均方误差损失:
$$L(\theta) = \mathbb{E}[(r + \gamma \max_{a'} Q(s', a'|\theta^-) - Q(s,a|\theta))^2]$$
为了稳定训练,DQN采用了经验回放和目标网络等技巧。
3. 部分可观测性
在实际环境中,智能体往往无法获得完整的系统状态信息,这就导致了部分可观测马尔可夫决策过程(POMDP)。POMDP可以用一个6元组$(S,A,P,R,\Omega,O. $描述,其中$\Omega$是观测空间,$O$是观测函数。✅
标准的DQN无法有效处理POMDP,因为它直接从观测估计Q值:$Q(o,a|\theta) \neq Q(s,a|\theta)$。
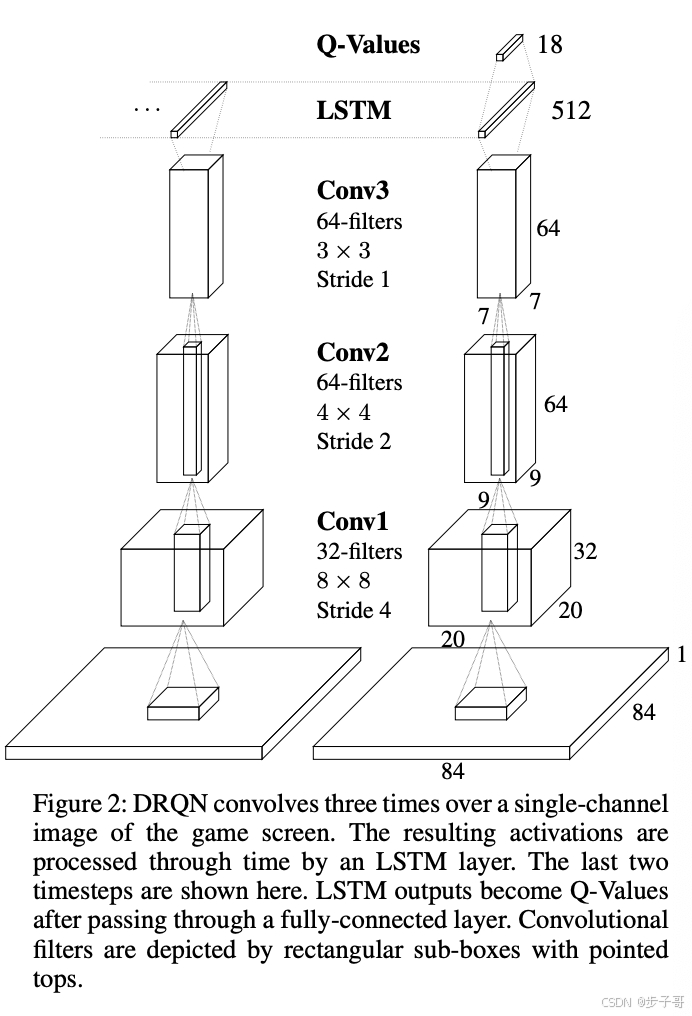
4. DRQN架构
DRQN在DQN的基础上,将第一个全连接层替换为LSTM层:
1) 输入:84x84的游戏画面
2) 3个卷积层
3) LSTM层(512个单元)
4) 全连接输出层(18个动作的Q值)
训练时同时学习卷积层和递归层的参数。
5. 稳定的递归更新
考虑了两种更新方式:
1) 顺序更新:从回放记忆中选择完整的episode进行更新
2) 随机更新:从回放记忆中随机选择起始点,更新固定步数
实验表明两种方式都可以收敛,本文采用随机更新方式。
6. Atari游戏:MDP还是POMDP?
Atari 2600游戏的状态可以由128字节的控制台RAM完全描述。但是,人类和AI智能体只能观察到游戏画面。对于许多游戏来说,单帧画面不足以确定系统状态。
DQN通过使用最近4帧画面作为输入来推断完整状态。为了引入部分可观测性,本文提出了"闪烁Pong"游戏 - 以0.5的概率遮挡每一帧画面。
7. 在标准Atari游戏上的评估
在9个Atari游戏上评估了DRQN的性能。结果表明:
1) DRQN的整体表现与DQN相当
2) 在Frostbite和Double Dunk上DRQN表现更好
3) 在Beam Rider上DRQN表现较差
8. 从MDP到POMDP的泛化
研究了在标准MDP上训练的网络是否能泛化到POMDP。结果表明:
1) 在闪烁版游戏上,DRQN和DQN的性能都有下降
2) DRQN比DQN保留了更多原有性能
3) 递归控制器对缺失信息具有一定的鲁棒性
9. 相关工作
之前的工作主要集中在使用策略梯度方法训练LSTM来解决POMDP。本文的创新点在于:
1) 使用时序差分更新来自举动作值函数
2) 联合训练卷积层和LSTM层,可以直接从像素学习
10. 讨论与结论
主要结论:
1) DRQN能够整合多帧信息,检测物体速度等相关特征
2) 在闪烁Pong游戏上,DRQN比DQN更能处理部分可观测性
3) DRQN学到的策略可以泛化到完全可观测的情况
4) 在大多数游戏中,递归网络相比输入层堆叠帧并没有系统性的优势
未来工作可以进一步研究递归网络在Pong和Frostbite等游戏上表现更好的原因。
参考文献
- Mnih, V. , Kavukcuoglu, K., Silver, D., et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529–533, 2015.✅
- Hochreiter, S. and Schmidhuber, J. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.✅
- Watkins, C. J. C. H. and Dayan, P. Q-learning. Machine learning, 8(3-4):279–292, 1992.✅
- Bellemare, M. G., Naddaf, Y., Veness, J., and Bowling, M. The arcade learning environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research, 47:253–279, 2013.✅
- Zeiler, M. D. ADADELTA: An adaptive learning rate method. arXiv preprint arXiv:1212.5701, 2012.✅